What is T test and z test?

When we want to do the hypothesis test i.e reject or accept the hypothesis basis on statistics then we use t test or z test.

Criteria to use t test or z test:

when number of samples are <=30 and population standard deviation is unknown, we use t test

else we go with z test.

in both tests, we have score and critical value.

note: we calculate score by using the formula and calculate critical value for t test using table.

*

In the above problem statement, we have population standard deviation but number of samples are greater than 30 hence we'll use z test.

we have to reject or accept null hypothesis at the 95% confidence level.

so for 95% critical value will be -1.96 and 1.96.

score = (sample mean - population mean) / (sample standard deviation / sqrt(number of samples))

if our score goes beyond critical value then we'll reject null hypothesis. (here null hypothesis is machine dispenses 80 ml of fluid)

* 

In this problem statement our alternate hypothesis is either it is less that 2 (it is not the not equal to 2)

hence we have at only 1 side because it is ok, if life span is >2 hence we have only 1 side.

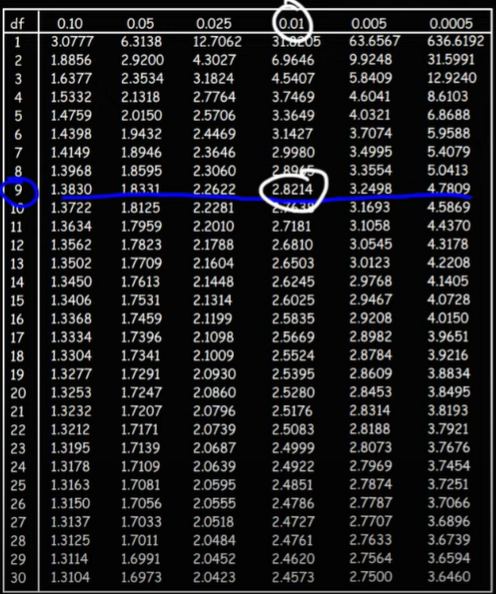
here for 99% confidence level i.e. for 0.01 p value and sample size of 10 our critical value which we get from t value table is,

while calculating we take degree of freedom (sample size -1) 

critical is 2.8214 and since it is on left side it becomes -2.8214.

and score we get from formula is -4.22

since t<score we reject null hypothesis.